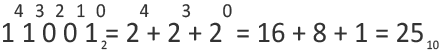ЕГЭ 2019 по информатике задание 6
Тема: «Выполнение и анализ простых алгоритмов».
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конец числа (справа) дописывается сначала ноль, а затем единица. В противном случае, если N нечётное, справа дописывается сначала единица, а затем ноль.
Например, двоичная запись 100 числа 4 будет преобразована в 10001,а двоичная запись 111 числа 7 будет преобразована в 11110.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R – результата
работы данного алгоритма.
Укажите минимальное число R, которое больше 102 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.
Данный пример взят из демоверсии 2019 по информатике на сайте http://fipi.ru
РЕШЕНИЕ
В начале определимся с числами N и R.
Число N — это то исходное число, которое вводится в автомат. Число R — это число, которое является результатом работы автомата.
В задаче 102 — это число R, поэтому для начала найдем число N, из которого и получилось число 102. Переведем 102 в двоичную систему счислений с помощью двух способов:
После перевода в двоичную систему число 102 будет выглядеть так 1100110. В задании сказано:
К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конец числа (справа) дописывается сначала ноль, а затем единица. В противном случае, если N нечётное, справа дописывается сначала единица, а затем ноль.
Это означает, что последние два числа 1100110 являются результатом работы автомата. Убираем числа 10 и получаем исходное число N(11001), которое было введено в автомат.
Переведем число 11001 в десятичную систему счислений:
Число 11001 нечётное, т.к. в двоичной записи оканчивается на 1. Если добавить число в автомат, то получим 1100110 (102). Это число не подходит под нашу задачу:
Укажите минимальное число R, которое больше 102 и может являться результатом работы данного алгоритма
Из этого следуют, что число N должно быть чётным, т.е. 26. Переведем 26 в двоичную систему: 11010
Далее произведем работу автомата: к числу 11010 добавим 01 и получим число 1101001. Переведем двоичное число 1101001 в десятичную систему счислений и получим результат 105. Число 105 является минимальным результатом работы автомата R.
Ответ: 105
[newsletter_signup_form id=1]