Построить таблицу истинности для логического выражения. Информатика в 8 классе.
Тема: «Основы алгебры логики».
Основы алгебры логики
Основы алгебры логики на уроках информатики изучаются в школе, начиная с 8 класса.
Прежде чем приступить к выполнению задания, разберем базовые понятия алгебры логики.
Алгебра логики (алгебра высказываний) — это формальная логическая теория, раздел математической логики. Основание алгебры логики положил Джордж Буль (1815 — 1864), развил же и усовершенствовал её Эрнст Шрёдер (1841-1902).
Высказывание — это предложение, о котором имеет смысл утверждать, истинно оно или ложно. Истина = 1, ложь =0.
Высказывание, включающее другие высказывания, называют сложным. Для образования сложных высказываний используют логические операции (связки).
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых.
Логические операции в порядке приоритета.
- Инверсия (отрицание)
- Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно.
В выражениях обозначается ¬A или A.
Читается «НЕ» (например, «не А»). - Конъюнкция (логическое умножение)
- Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания.
В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB).
Читается «И» (например, «А и Б») - Дизъюнкция (логическое сложение)
- Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний.
В выражениях обозначается A ∨ B, иногда A + B.
Читается «ИЛИ» (например, «А или Б») - Импликация (следование)
- Импликация — это логическая операция, образующая сложное высказывание, ложное тогда и только тогда, когда первое исходное высказывание истинно, а второе — ложно.
В выражениях обозначается A ⇒ B или A → B.
Читается «ЕСЛИ…ТО» (например, «если А, то Б») - Эквивалентность (равнозначность)
- Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают.
В выражениях обозначается A ⇔ B или A ≡ B.
Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)
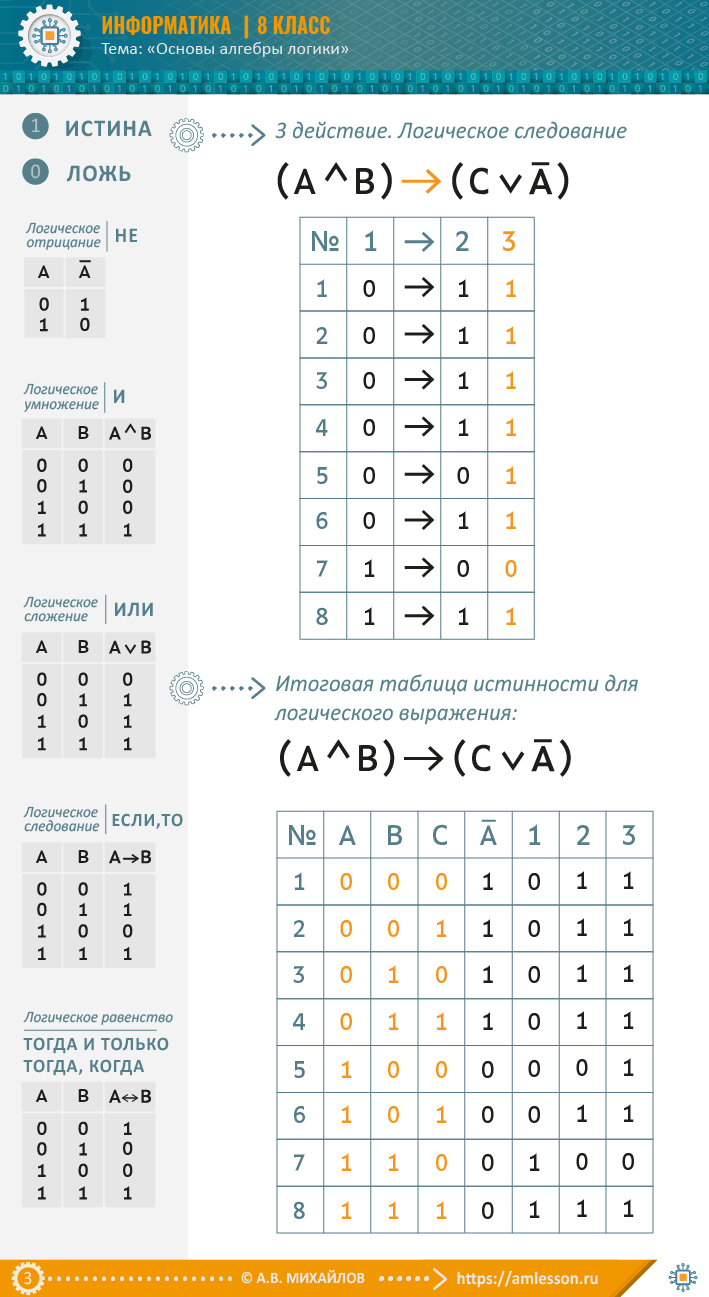
Для записи логических функций часто используют таблицы истинности.
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.